P-SPECTRAL CLUSTERING
by Thomas Bühler and Matthias Hein
In recent years, spectral clustering has evolved into one of the major clustering methods and has found applications in a wide range of areas. The key idea of spectral clustering is to approximate the optimal cluster indicator function by the second eigenvector of the well-known graph Laplacian. This approach can be motivated as a relaxation of balanced graph cuts. However, the quality guarantees given on this standard relaxation are relatively weak, and in fact there exist examples where this approximation and the resulting clustering is clearly suboptimal (see below for an example).
In the paper "Spectral Clustering based on the graph p-Laplacian", we proposed a generalized version of spectral clustering based on the second eigenvector of the graph p-Laplacian, a nonlinear generalization of the graph Laplacian. We showed that it can also be derived as a relaxation of balanced graph cuts. Our generalized version of spectral clustering yields standard spectral clustering as special case for p=2. Interestingly, one can show that spectral clustering based on the graph p-Laplacian for p->1 generally has a superior performance compared to standard spectral clustering, in terms of minimizing the normalized/ratio Cheeger cut criterion.
| p=2.0 | p=1.7 | p=1.4 | p=1.1 | |
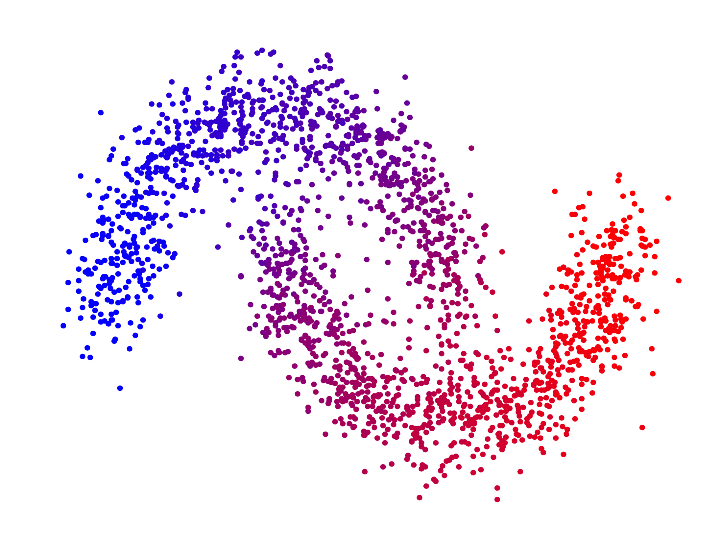
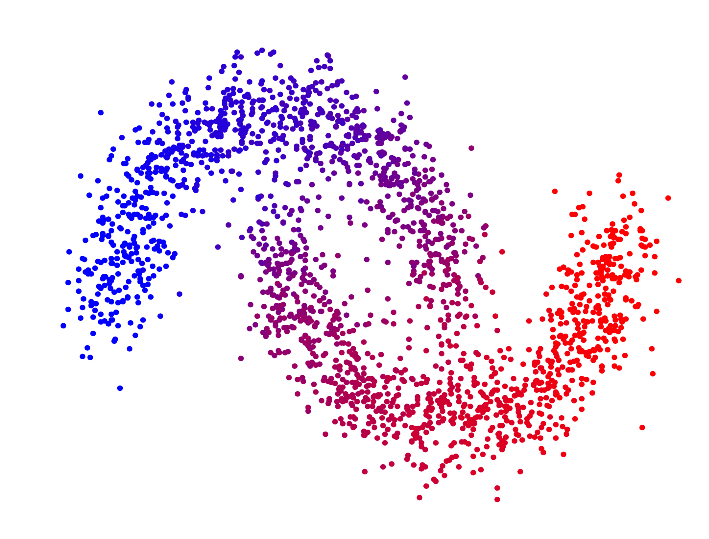
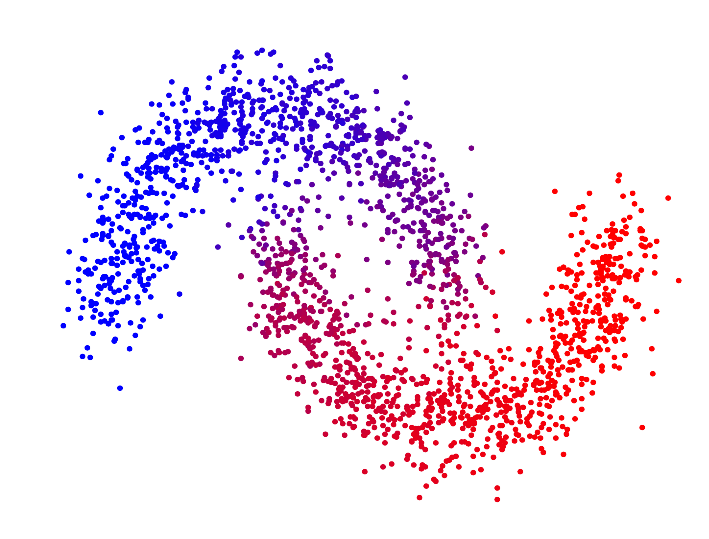
| Second eigenvector of the p-Laplacian |
|
|
|
|
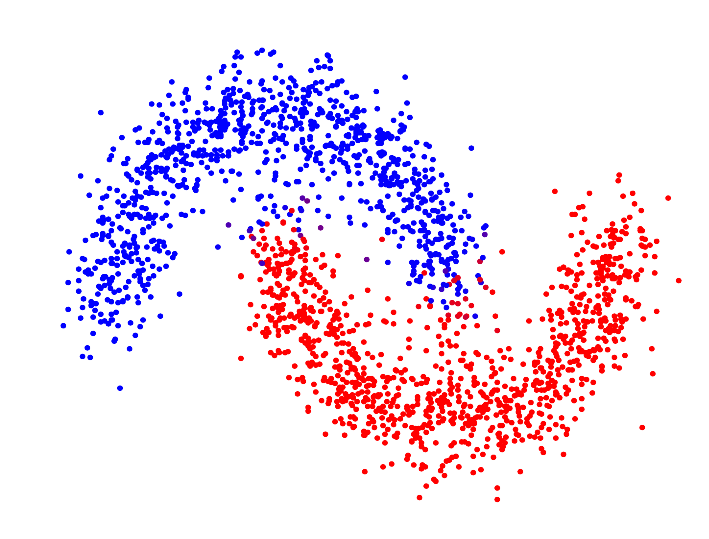
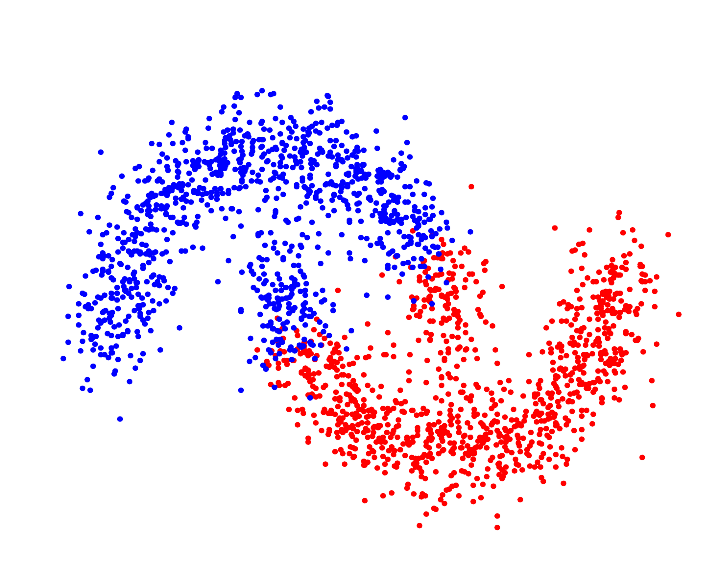
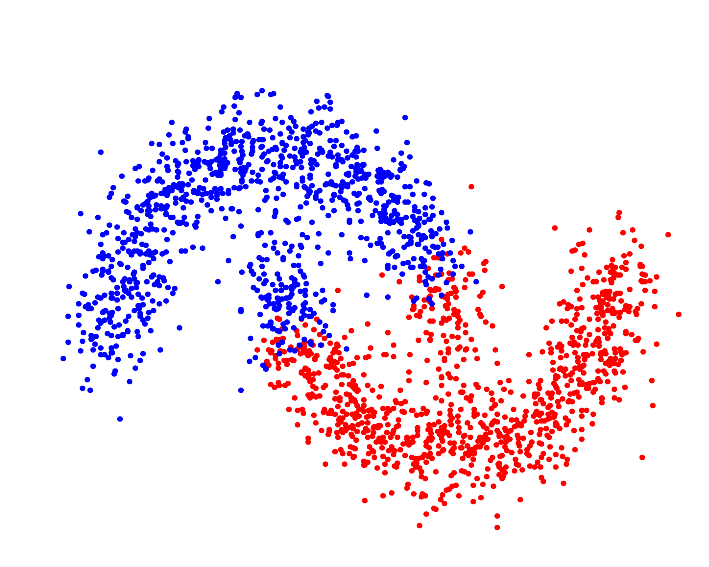
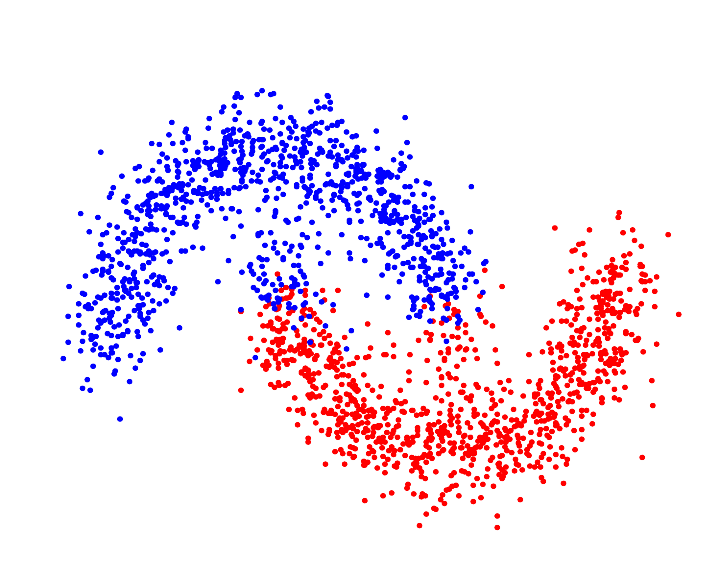
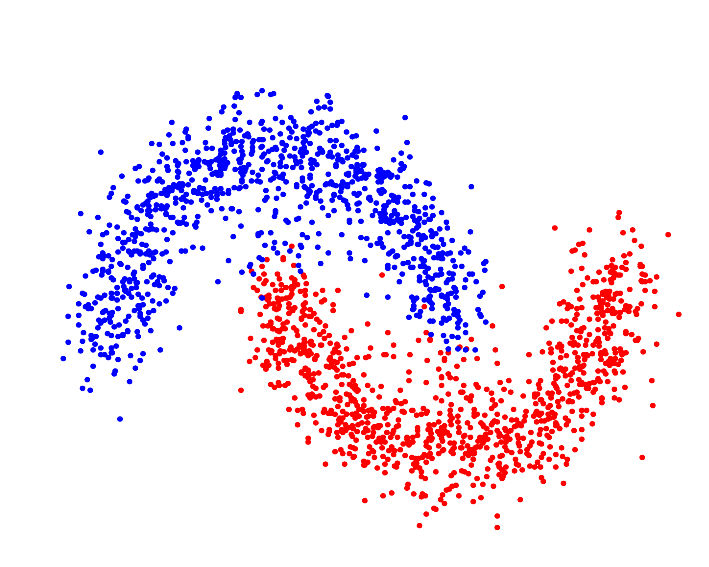
| Resulting clustering |
|
|
|
|
For p->1 the eigenvector of the graph p-Laplacian yields a better approximation of the optimal cluster indicator function, thus leading to decreasing cut values. In fact one can show that in the limit of p->1, the cut found by thresholding the second eigenvector of the graph p-Laplacian converges to the optimal normalized/ratio Cheeger cut.
We proposed a numerical scheme to compute the second eigenvector of the p-Laplacian and the resulting clustering, an implementation of which can be found on this website.
NEWS
While the method available on this page is based on the second eigenvector of the graph p-Laplacian only for p>1, we recently developed an improved method based on the eigenvectors of the graph 1-Laplacian, which can be computed using our nonlinear inverse power method. The new method runs faster and produces better cuts. Click here to download code for 1-Spectral Clustering.
DOWNLOAD AND LICENSE
p-Spectral Clustering has been developed by Thomas Bühler and Matthias Hein, Department of Computer Science, Saarland University, Germany. The code for p-Spectral Clustering is published as free software under the terms of the GNU GPL v3.0. Please include a reference to the paper Spectral Clustering based on the graph p-Laplacian and include the original documentation and copyright notice.
Download pSpectral Clustering ![]() (Version: 1.1)
Version history
(Version: 1.1)
Version history
REFERENCES
T. Bühler, M. Hein,
Spectral Clustering based on the graph p-Laplacian,
In Leon Bottou and Michael Littman, editors, Proceedings of the 26th
International Conference on Machine Learning (ICML 2009), 81-88, Omnipress, 2009, PDF ![]() (Supplementary material: PDF
(Supplementary material: PDF ![]() - Errata of Supp. Mat.: PDF
- Errata of Supp. Mat.: PDF ![]() )
)
INSTALLATION
To run p-Spectral Clustering, download the archive and unzip it in some convenient directory. Then run the script make.m to compile the mexfiles. The eigenvector and resulting clustering can then be computed by the functions 'computePEigenvector' and 'pSpectralClustering', respectively. If you find bugs or have other comments contact Thomas Bühler or Matthias Hein.
DOCUMENTATION
Computation of p-Spectral Clustering (main method):
[clusters,cuts,cheegers,vmin,fmin,normGrad] = pSpectralClustering(W,p,normalized,k)
Computes a multipartitioning using the recursive splitting scheme described in the paper. Performs p-Spectral Clustering into k clusters of the graph with weight matrix W by using the second eigenvector of the unnormalized/normalized graph p-Laplacian.
W: Sparse symmetric mxm weight matrix.
p: Has to be in the interval ]1,2].
normalized: True for Ncut/NCC, false for Rcut/RCC.
k: number of clusters
clusters: mx(k-1) matrix containing in each column the computed clustering for each partitioning step.
cuts: (k-1)x1 vector containing the Ratio/Normalized Cut values after each partitioning step.
cheegers: (k-1)x1 vector containing the Ratio/Normalized Cheeger Cut values after each partitioning step.
vmin: Second eigenvector of the graph p-Laplacian for the first partitioning step.
fmin: Second eigenvalue of the graph p-Laplacian for the first partitioning step.
normGrad: Norm of the gradient after the first partitioning step.
Computation of the second eigenvector of the graph p-Laplacian:
[vmin,fmin,umin,normGrad] = computePEigenvector(W,p,normalized)
[vmin,fmin,umin,normGrad] = computePEigenvector(W,p,normalized,v_old,p_old)
[vmin,fmin,umin,normGrad] = computePEigenvector(W,p,normalized,v_old)
Computes the second p-eigenvector of the graph p-Laplacian of the graph with weight matrix W using the iterative scheme introduced in the paper. As described in the paper, the iterative scheme is initialized with the second eigenvector of the standard graph Laplacian (p=2). However one can also provide an initialization with the second p_old-eigenvector v_old, or with an arbitry vector v_old.
W: Sparse symmetric mxm weight matrix.
p: Has to be in the interval ]1,2].
normalized: True for normalized p-Laplacian, false for unnormalized p-Laplacian.
v_old: Optional initialization. Default: Second eigenvector of the standard graph Laplacian.
p_old: Optional start value for reduction of p. Has to be in the interval ]p,2]. Default: 2.
vmin: Second eigenvector of the normalied/unnormalized graph p-Laplacian.
fmin: Second eigenvalue of the normalied/unnormalized graph p-Laplacian.
umin: Minimizer of the functional F_2.
normGrad: Norm of the gradient.
Computation of cluster indicator function:
[clusters, cut,cheeger,cutPart1,cutPart2,threshold] = createClusters(vmin,W,normalized,threshold_type,criterion)
Transforms an eigenvector vmin into a clustering.
W: Sparse symmetric mxm weight matrix.
vmin: Vector to be thresholded.
normalized: True for Ncut/NCC, false for Rcut/RCC.
threshold_type: 0: zero, 1: median, 2: mean, -1: best
criterion: Criterion to be optimized in thresholding. 1: Normalized/Ratio Cheeger Cut. 2: Normalized/Ratio Cut. 3: Cut with maximal 5% imbalance.
clusters: Obtained clustering after thresholding.
cut: Value of the Normalized/Ratio Cut.
cheeger: Value of the Normalized/Ratio Cheeger Cut.
cutpart1,cutpart2: The two components of Ratio/Normalized Cut and Ratio/Normalized Cheeger Cut.
threshold: The threshold used to obtain the partitioning.