SEMI-SUPERVISED REGRESSION USING HESSIAN ENERGY
ABOUT
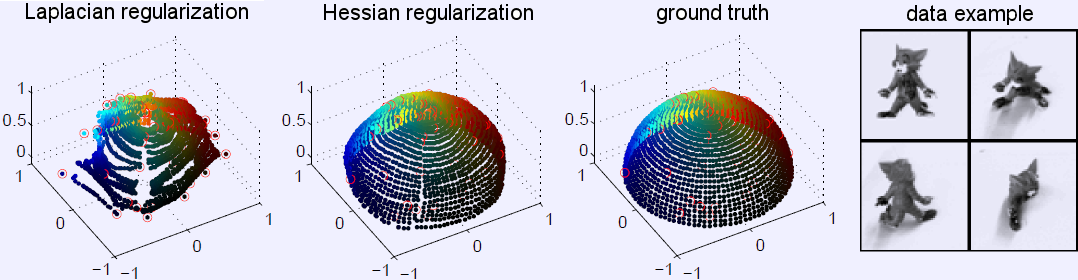
Semi-supervised regression based on the graph Laplacian suffers from the fact that the solution is biased towards a constant and the lack of extrapolating power (Fig. 1).Based on these observations, we propose to use the second-order Hessian energy for semi-supervised regression which overcomes both these problems. If the data lies on or close to a low-dimensional submanifold in feature space, the Hessian energy prefers functions whose values vary linearly with respect to geodesic distance. The preference of "linear functions" on manifolds renders the Hessian energy particularly suited for the task of semi-supervised dimensionality reduction, where the goal is to find a user-defined embedding function given some labeled points which varies smoothly (and ideally linearly) along the manifold (see title image and Fig. 2 for example).
The proposed Hessian energy is motivated by the recently proposed Eells energy for mappings between manifolds [1], which contains as a special case the regularization of real-valued functions on a manifold. In flavor, it is also quite similar to the operator constructed in Hessian eigenmaps [2]. However, their operator due to problems in the estimation of the Hessian, leads to useless results when used as regularizer for regression.
Using this novel technique, we have constructed systems comparable to state-of-the-art systems for image colorization and human pose estimation (details can be found in [3]).
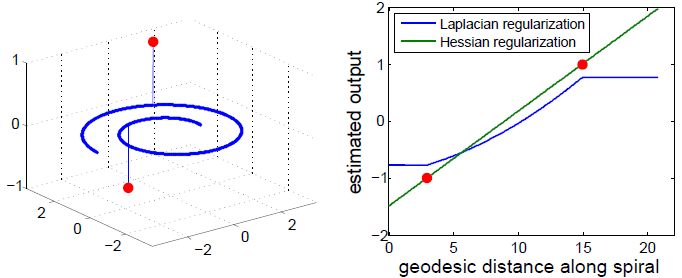
Figure 1: Difference between semi-supervised regression using Laplacian and Hessian regularization for fitting two points on the one-dimensional spiral (Left). The Laplacian regularization has always a bias towards the constant function and the extrapolation beyond data points to the boundary of the domain is always constant (Right). On the contrary the Hessian regularization extrapolates nicely to unseen data, since it's null space contains functions which vary linearly with the geodesic distance.

Figure 2: Results of regression on the artificial
digit 1 dataset with four variations (horizontal and vertical translations,
thickness variation, and rotation). 21 digit images sampled at regular
intervals on the line between (0,0,0,0) and (1,1,1,1) in the resulting four
dimensional parameter space. ‘KRR’: kernel ridge regression, ‘Laplacian’:
semi-supervised regression using Laplacian regularization, and ‘Hessian’:
semi-supervised regression using Hessian regularization as described in our
paper.
CODE
Download ![]() a Matlab code.
a Matlab code.
Download ![]() digit data (see Matlab code for details).
digit data (see Matlab code for details).
REFERENCES
| [1] | F. Steinke, M. Hein, J. Peters, B. Schoelkopf, "Manifold-valued thin-plate splines with applications in computer graphics", Computer Graphics Forum, vol. 27, pp. 437-448, 2008. |
| [2] | D. Donoho and C. Grimes, "Hessian eigenmaps: locally linear embedding techniques for high-dimensional data", Proc. of the National Academy of Sciences, vol. 100, no. 10, pp. 5591-5596, 2003. |
| [3] | K. I. Kim, F. Steinke, and M.
Hein, "Semi-supervised
regression using Hessian energy with an application to semi-supervised
dimensionality reduction |
CONTACT
Kwang In Kim: kimki@cs.uni-sb.de
Florian Steinke: Florian.Steinke@siemens.com
Matthias Hein: hein@cs.uni-sb.de