INVERSE POWER METHOD FOR NONLINEAR EIGENPROBLEMS
by Matthias Hein and Thomas Bühler
NONLINEAR EIGENPROBLEMS IN MACHINE LEARNING
Many problems in machine learning and statistics can be formulated as (generalized) eigenproblems. Linear eigenvectors correspond to critical points of a ratio of quadratic functionals
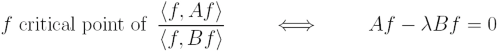
Nonlinear eigenvectors correspond to critical points of a ratio of general functionals R and S which we assume to be convex and p-homogeneous.

OUR NONLINEAR IPM FOR NONLINEAR EIGENPROBLEMS
In the paper [1] we proposed a nonlinear inverse power method to compute solutions of the nonlinear eigenproblems above. While our inverse power method is a general purpose method, we showed for two unsupervised learning problems that it can be easily adapted to a particular application. Below you find applications of our method for 1-Spectral Clustering and Sparse PCA. In both applications we achieve state-of-the-art results in terms of solution quality and runtime.
APPLICATIONS
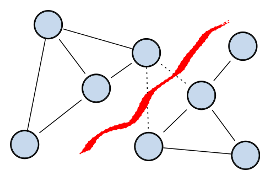 |
Cheeger cut minimization and 1-Spectral ClusteringIn [1] we showed that the second eigenvalue of the nonlinear graph 1-Laplacian is equal to the optimal Cheeger cut. Our nonlinear inverse power method can be applied to efficiently compute nonconstant nonlinear eigenvectors of the graph 1-Lapacian and the resulting 1-spectral clustering. |
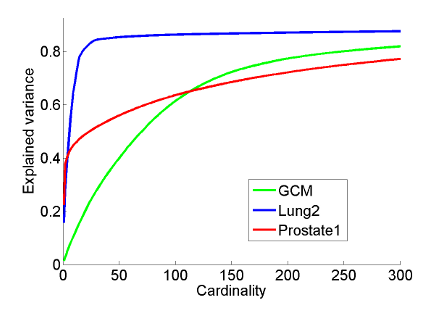 |
Sparse Principal Component AnalysisSparse PCA tries to avoid the disadvantage of classical PCA of noninterpretability of the principal components by enforcing sparsity of the solution. As shown in [1], Sparse PCA can be modelled as a nonlinear eigenproblem and efficiently be solved by our nonlinear IPM. |
REFERENCES
[1] M. Hein and T. Bühler,
An inverse power method for nonlinear eigenproblems with applications in 1-spectral clustering and sparse PCA,
In Advances in Neural Information Processing Systems 23 (NIPS 2010), 847-855, 2010. PDF ![]() (Supplementary material: PDF
(Supplementary material: PDF ![]() )
)