POWER METHOD FOR THE MAXIMAL  -SINGULAR VALUE OF NON-NEGATIVE TENSORS
-SINGULAR VALUE OF NON-NEGATIVE TENSORS
by Antoine Gautier and Matthias Hein
TENSOR PROJECTIVE NORM
Given a tensor of ![]() order m and
order m and ![]() , we propose in our paper, a power method type algorithm for computing a maximizer of the following problem:
, we propose in our paper, a power method type algorithm for computing a maximizer of the following problem:
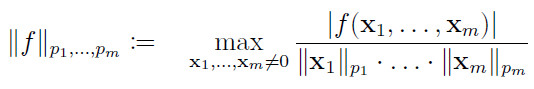
where ![]() denotes the usual pi-norm on
denotes the usual pi-norm on ![]() and
and ![]() is the multi-linear form associated to the tensor
is the multi-linear form associated to the tensor ![]() , i.e.
, i.e.
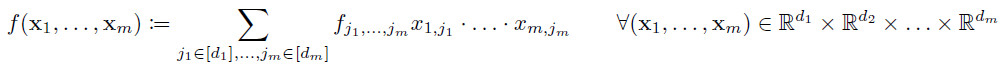
with ![]() .
.
Matrix case: When the tensor is of order m = 2, i.e. ![]() is a matrix, the maximization problem above reduces to the so-called matrix p, q-norm, namely
is a matrix, the maximization problem above reduces to the so-called matrix p, q-norm, namely
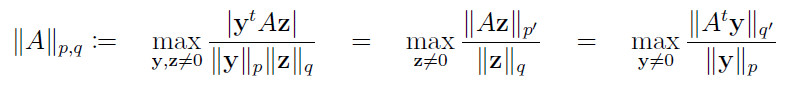
with ![]() .
.
Remark 1. Provided that the convergence assumptions are fulfilled, the algorithm produces two monotonic sequences ![]() such that
such that
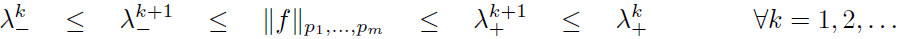
and thus can also be used to simply obtain an upper bound on ![]() .
.
CONVERGENCE GUARANTEE
The method is guaranteed to converge to a global maximizer of the optimization problem above if:
a) ![]() is non-negative, i.e.
is non-negative, i.e. ![]() for all
for all ![]() .
.
b) ![]() and there exists
and there exists ![]() such that
such that
Example:
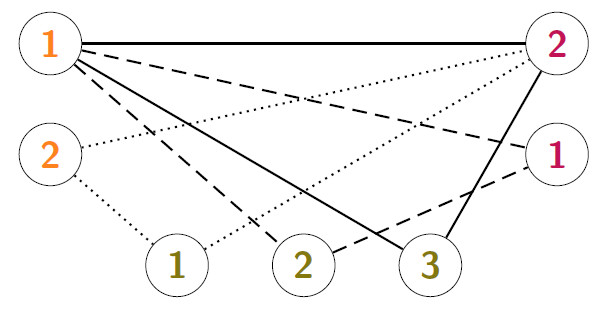
c) The tensor ![]() is weakly irreducible. That is, the undirected m-partite graph G(T) = (V,E) is connected where
is weakly irreducible. That is, the undirected m-partite graph G(T) = (V,E) is connected where
is the disjoint union of
and
such that
Example:
with
and
Matrix case: When the tensor ![]() is a matrix, then the three conditions above reduce to:
is a matrix, then the three conditions above reduce to:
a) A is non-negative, i.e. ![]() for every
for every ![]() .
.
b) ![]() and
and ![]() .
.
c) A is weakly irreducible (see definition above).
Example: If ![]() ,
then the undirected graph G(A) is given by
,
then the undirected graph G(A) is given by
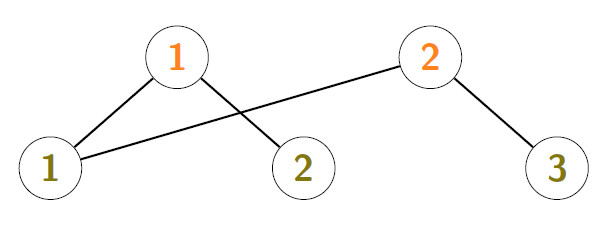
and therefore A is weakly irreducible because G(A) is connected.
DOWNLOAD AND LICENSE
Please include a reference to our preprint
- A. Gautier and M. Hein
Tensor norm and maximal singular vectors of non-negative tensors - a Perron-Frobenius theorem, a
Collatz-Wielandt characterization and a generalized power method
arXiv:1503.01273
if you find this code useful for your research.