Saarland University, Machine Learning Group, Fak. MI - Mathematik und Informatik, Campus E1 1, 66123 Saarbrücken, Germany     

Machine Learning Group
Department of Mathematics and Computer Science - Saarland University

CONSTRAINED 1-SPECTAL CLUSTERING

by Syama Sundar Rangapuram and Matthias Hein

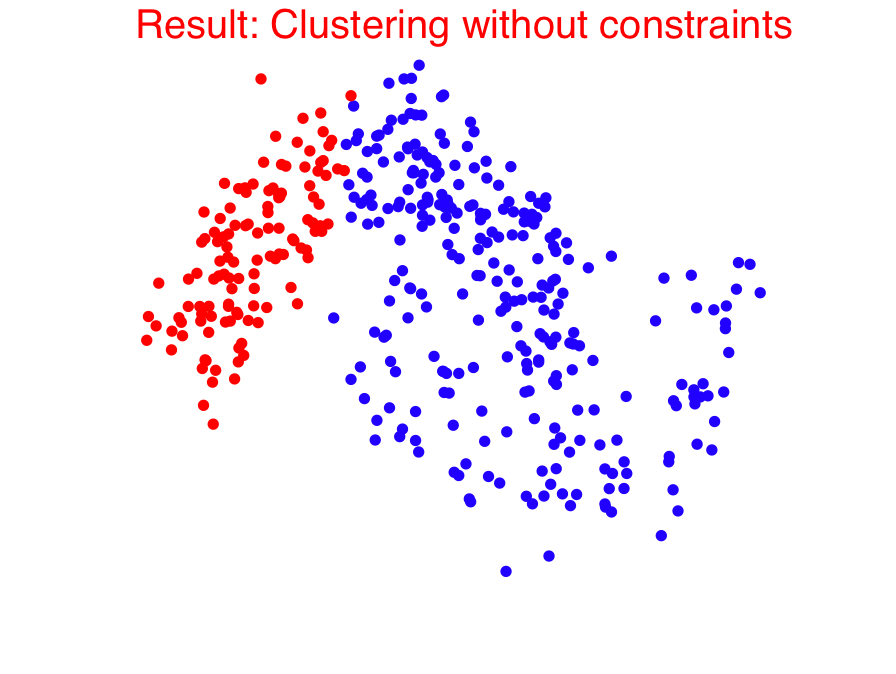
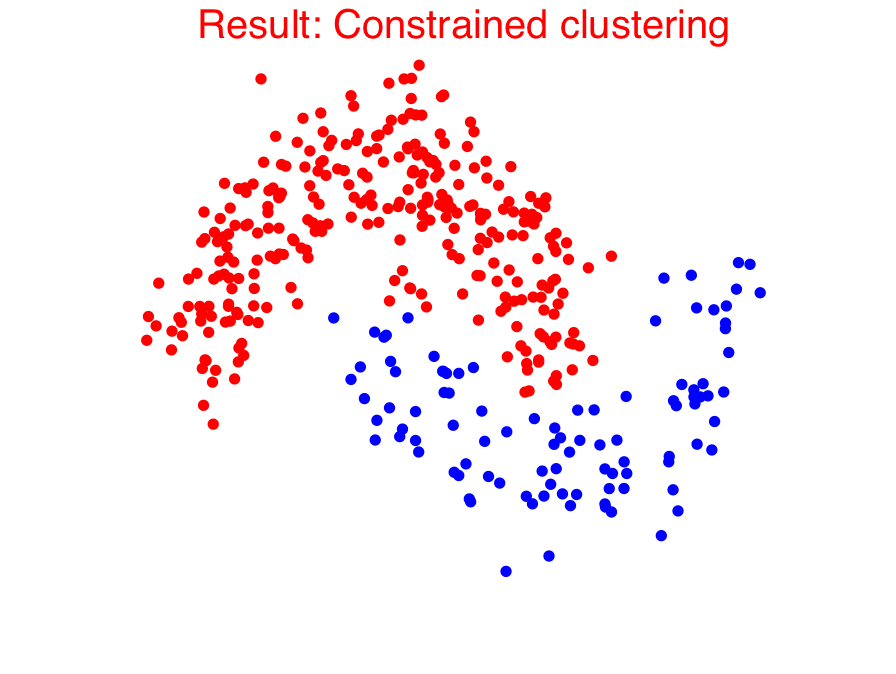
An important form of prior information in clustering comes in the form of must-link and cannot-link constraints. In the paper [1], we presented a generalization of the popular spectral clustering technique to integrate such constraints. Motivated by the recently proposed 1-spectral clustering [2], our method is based on a tight relaxation of the constrained normalized cut problem into a continuous optimization problem. In contrast to the existing constrained spectral clustering methods, we can always guarantee to satisfy all constraints. Moreover, our soft formulation also allows to optimize a trade-off between normalized cut and the number of violated constraints. Our efficient implementation, that scales to large datasets, shows that our method consistently outperforms all the other proposed methods.

DOWNLOAD AND LICENSE

Constrained 1-Spectral Clustering has been developed by Syama Sundar Rangapuram, Max Planck Institute for Computer Science and Matthias Hein, Department of Computer Science, Saarland University, Germany. The Matlab code for Constrained 1-Spectral Clustering is published as free software under the terms of the GNU GPL v3.0. Please include a reference to the paper Constrained 1-Spectral Clustering and include the original documentation and copyright notice.

Download Constrained 1-SpectralClustering Code       (Version: 1.1, Matlab/C Code)

Unzip the file cosc_v1_1.zip and see README.txt to setup and run the program. If there is any problem using this code, contact Syama Sundar Rangapuram: srangapu@mpi-inf.mpg.de

REFERENCES

[1] S. Rangapuram and M. Hein,
Constrained 1-Spectral Clustering,
In International conference on Artificial Intelligence and Statistics (AISTATS), 2012. PDF  (Long version: PDF )

[2] M. Hein and T. Bühler,
An inverse power method for nonlinear eigenproblems with applications in 1-spectral clustering and sparse PCA,
In Advances in Neural Information Processing Systems 23 (NIPS 2010), accepted. PDF  (Supplementary material: PDF )