A FLEXIBLE TENSOR BLOCK COORDINATE ASCENT SCHEME FOR HYPERGRAPH MATCHING
by Quynh Nguyen, Antoine Gautier and Matthias Hein
DOWNLOAD
Please include a reference to our paper
- Q. Nguyen, A. Gautier and M. Hein
A Flexible Tensor Block Coordinate Ascent Scheme for Hypergraph Matching
CVPR 2015 (oral presentation). PDF Supplement: PDF
Supplement: PDF  Extended Abstract: PDF
Extended Abstract: PDF  Poster: PDF
Poster: PDF  Slide: PDF
Slide: PDF 
if you find this code useful for your research.
Download tensor_bcagm_v10.tar.gz ![]() (Size:41.4 MB)
(Version: 1.0, Matlab/C Code)
(Size:41.4 MB)
(Version: 1.0, Matlab/C Code)
Extract the file ’tensor bcagm v10.tar.gz’ and see README.txt to setup and run the program. If there is any problem using this code, contact Quynh Nguyen: quynh@cs.uni-saarland.de
 (a) 34 pts vs 44 pts, 10 outliers |
 (b) TM 10/34 (1715.0) |
|
 (c) HGM 9/34 (614.7) |
 (d) RRWHM 28/34 (5230.5) |
|
 (e) our BCAGM 28/34 (5298.8) |
 (f) our BCAGM+MP 34/34 (5377.3) |
Figure 1: Car dataset with outlier test: a) Input images. Blue dots denote outlier nodes. The number of correct matches and the objective score are reported for each hypergraph matching algorithm.
INTRODUCTION
The estimation of correspondences between two images resp. point sets is a core problem in computer vision. One way to formulate the problem is graph matching leading to the quadratic assignment problem which is NP-hard. Several so-called second order methods [3, 2, 6, 7, 10, 8] have been proposed to solve this problem. In recent years, hypergraph matching leading to a 3rd order polynomial optimization problem [1, 4, 5, 9] became popular as it allows for better integration of geometric information. However, for most of these 3rd order algorithms there is a lack of theoretical guarantees and analysis.
In this paper, we propose a general optimization framework based on tensor block coordinate ascent for hypergraph matching. We propose two algorithms which both come along with the guarantee of monotonic ascent in the matching score on the set of discrete assignment matrices. The main idea of our framework is to optimize the multilinear form instead of the original score function. In particular, we theoretically prove the equivalence between the optimization
of the score function and the optimization of its associated multilinear form over any constraint set. This allows
us to directly handle the original constraint set without the need of relaxation. Furthermore, we prove two important
inequalities which show that obtaining ascent in the multilinear form also means obtaining ascent in the original
score function. Comparative experiments show that our new algorithms outperform previous work both in terms of
achieving better matching scores and matching accuracy. This holds in particular for very challenging settings where one
has a high number of outliers and other forms of noise.
 |
 |
|
 |
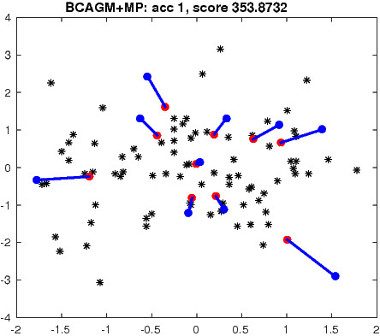 |
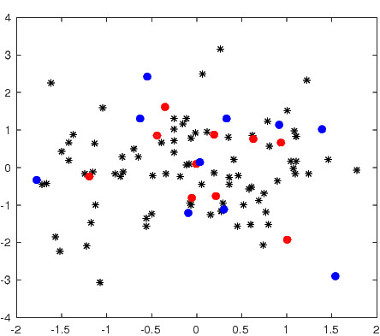
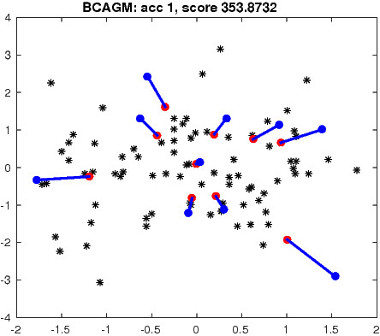
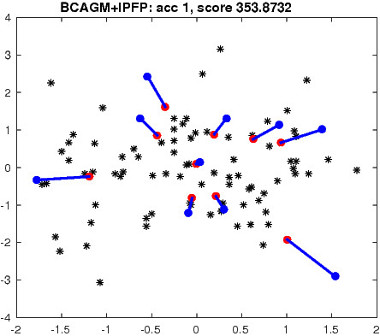
Figure 2: Top left: an example of matching task in R 2 . Blue/red dots correspond to two point sets. Black dots denote outlier points. The number of correct matches and the objective score are reported for each algorithm. Blue/red lines indicate correct/incorrect matches.
EXPERIMENTAL RESULTS
We refer to our paper for the full experiments and show below some results for the CMU house dataset, which is a standard benchmark for graph matching. For comparison with state-of-the-art higher order algorithms, we use Tensor Matching (TM) [4], Hypergraph Matching via Reweighted Random Walks (RRWHM) [5] and Hypergraph Matching (HGM) [9]. For second order methods, we compare our algorithms with Max Pooling Matching (MPM) [3], Reweighted Random Walks for Graph Matching (RRWM) [2], Integer Projected Fixed Point (IPFP) [7], Spectral Matching (SM) [6]. We denote different algorithm variants of our tensor block coordinate ascent scheme as BCAGM, BCAGM+MP and BCAGM+IPFP.
CMU House Dataset
In this dataset, 30 landmark points are manually tracked over a sequence of 111 images, which are taken from the same object under different view points. In this experiment, baseline denotes the distance of the frames in the sequence and thus correlates well with the difficulty to match the corresponding frames. We matched all possible image pairs with baseline of 10,20,30,...,100 frames and computed the average matching accuracy for each algorithm. The algorithms are evaluated in three settings. In the first experiment, we match 30 points to 30 points. Then we make the problem significantly harder by randomly removing points from one image motivated by a scenario where one has background clutter in an image and thus not all points can be matched. This results in two matching experiments, namely 10 points to 30 points, and 20 points to 30 points.
 (a) An input pair: 10 pts vs 30 pts, baseline = 50 |
 (b) MPM 4/10 (15.6) |
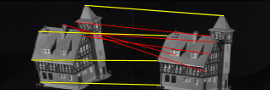 (c) TM 5/10 (18.4) |
 (d) RRWHM 7/10 (26.4) |
 (e) BCAGM 10/10 (43.1) |
 (f) BCAGM+MP 10/10 (43.1) |
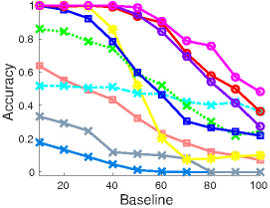 (g) 10 pts vs 30 pts |
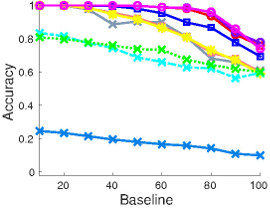 (h) 20 pts vs 30 pts |
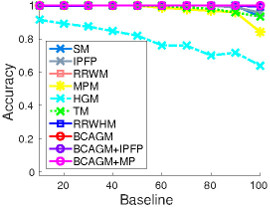 (i) 30 pts vs 30 pts |
Figure 3: CMU house dataset: The first two rows show the matching results of several algorithms on an example input. The yellow/red lines indicate correct/incorrect matches. The third row shows the average performance of matching algorithms with different number of points in the first image. Note that decreasing the number of points in the first image is equivalent to having more outliers in the second image.
REFERENCES
[1] M. Chertok and Y. Keller. Efficient high order matching. PAMI, 32:2205–2215, 2010. 1
[2] M. Cho, J. Lee, and K. M. Lee. Reweighted random walks for graph matching. In ECCV, 2010. 1 2
[3] M. Cho, J. Sun, O. Duchenne, and J. Ponce. Finding matches in a haystack: A max-pooling strategy for graph matching in the
presence of outliers. In CVPR, 2014. 1 2
[4] O. Duchenne, F. Bach, I. Kweon, and J. Ponce. A tensor-based algorithm for high-order graph matching. PAMI, 33:2383–2395,
2011. 1 2
[5] J. Lee, M. Cho, and K. M. Lee. Hyper-graph matching via reweighted random walks. In CVPR, 2011. 1 2
[6] M. Leordeanu and M. Hebert. A spectral technique for correspondence problems using pairwise constraints. In ICCV, 2005. 1 2
[7] M. Leordeanu, M. Hebert, and R. Sukthankar. An integer projected fixed point method for graph matching and map inference. In NIPS, 2009. 1 2
[8] M. Zaslavskiy, F. Bach, and J. Vert. A path following algorithm for the graph matching problem. PAMI, 31:2227–2242, 2009. 1
[9] R. Zass and A. Shashua. Probabilistic graph and hypergraph matching. In CVPR, 2008. 1 2
[10] F. Zhou and F. De la Torre. Deformable graph matching. In CVPR, 2013. 1