SPARSE PCA
by Matthias Hein and Thomas Bühler
SPARSE PRINCIPAL COMPONENT ANALYSIS
 Principal Component Analysis (PCA) is a standard technique for dimensionality reduction and data analysis which finds the k-dimensional subspace of maximal variance in the data. However the interpretation of the PCA component is difficult as usually all components are nonzero.
Principal Component Analysis (PCA) is a standard technique for dimensionality reduction and data analysis which finds the k-dimensional subspace of maximal variance in the data. However the interpretation of the PCA component is difficult as usually all components are nonzero.
In sparse PCA one wants to get a small number of features which still capture most of the variance. Thus one needs to enforce sparsity of the PCA component, which yields a trade-off between explained variance and sparsity.
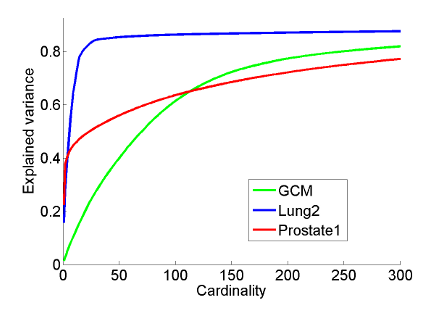
This plays a role for instance in the case of gene expression data where one would like the principal components to consist only of a few significant genes, making it easy to interpret by a human. The right plot shows the variance-cardinality tradeoff curve for three gene expression datasets.
As shown in [1], [2], Sparse PCA can be modelled as a nonlinear eigenproblem and efficiently be solved by our nonlinear IPM. An implementation can be downloaded from this website.
DOWNLOAD AND LICENSE
The nonlinear IPM for sparse PCA has been developed by Matthias Hein and Thomas Bühler, Department of Computer Science, Saarland University, Germany. The code for sparse PCA is published as free software under the terms of the GNU GPL v3.0. Please include a reference to the paper An inverse power method for nonlinear eigenproblems with applications in 1-spectral clustering and sparse PCA and include the original documentation and copyright notice.
Download sparsePCA ![]() (Matlab-Code, Version: 2.0)
Version history
(Matlab-Code, Version: 2.0)
Version history
REFERENCES
[1] M. Hein and T. Bühler,
An inverse power method for nonlinear eigenproblems with applications in 1-spectral clustering and sparse PCA,
In Advances in Neural Information Processing Systems 23 (NIPS 2010), 847-855, 2010. PDF ![]() (Supplementary material: PDF
(Supplementary material: PDF ![]() )
)
[2] T. Bühler,
A flexible framework for solving constrained ratio problems
in machine learning,
Ph.D. Thesis, Saarland University, 2015. PDF ![]()